이자율변동의 주택시장 파급효과 분석

Ⅰ. 서론

오랫동안 지속되던 저금리 시대가 끝나고 통화정책 기조는 금리 인상으로 방향을 전환하고 있다. 이자율 상승은 주택 수요 위축을 통해 주택시장에 부정적인 영향을 미치게 된다.¹⁾ 주택 수요의 감소는 주택가격을 하락시키고 주택거래량을 위축시키는 효과를 갖는다. 이자율 상승의 효과가 주택시장에서 구체적으로 얼마나 그리고 어떠한 시간 경로를 따라 실현되는가에 대한 분석은 거시 혹은 주택관련 경제정책 담당자, 주택소유자, 부동산투자자, 그리고 연구자들 모두에게 중요한 관심사이다.

본 연구에서는 이자율과 주택시장 변수들로 구성된 벡터자기회귀(VAR) 모형을 통해 이자율 변동이 주택시장에 미치는 영향을 분석한다. VAR 모형을 이용하여 이자율의 변동 효과를 다룬 국내의 대부분의 연구는 주택시장 변수로 주택거래량을 고려하지 않고 있다.²⁾ 주택거래량은 주택가격과 함께 주택시장을 구성하는 가장 기본적인 변수이다. 또한 두 변수간의 동적 연관성도 매우 높은 것으로 분석되고 있다.³⁾ 본 연구에서는 이를 감안하여 이자율, 주택가격, 주택거래량의 3변수로 구성된 VAR 모형을 설정하고, 이를 통해 이자율 변동이 주택시장에 미치는 효과를 구체적 수치를 통해 살펴보고자 한다. VAR 모형에서 통화, 소득, 물가 등의 거시경제 관련 통제변수를 부가함으로써 분석 결과의 정치성을 높일 수도 있겠으나, 그 차이가 본 연구에서의 분석결과를 훼손시킬 정도로 크지는 않을 것이라고 생각된다.⁴⁾ 본 연구에서는 이자율 변동이 주택시장에 미치는 직접적인 효과에 초점을 맞추어 모형을 단순화하였다.

VAR 모형을 통한 이자율 변동 효과 분석에서 쟁점 중의 하나는 이자율 충격을 어떻게 식별할 것인가의 문제이다.⁵⁾ 본 연구에서는 Uhlig(2005)의 부호제약(sign restriction) 방식을 이용하여 이자율 충격을 식별한다.⁶⁾ 부호제약에 의한 식별 방식은 통상적으로 많이 이용되는 촐레스키 분해의 한계점⁷⁾을 갖지 않으며, 이자율 변동에 따른 주택시장에의 파급효과를 특정한 수치가 아니라 일정한 범위로 나타냄으로써 보다 현실적인 분석 결과를 얻을 수 있는 장점을 갖는다. 본 연구에서는 촐레스키 분해를 이용한 분석결과도 함께 제시함으로써 부호제약에 의한 식별방식과의 차이도 살펴보았다.

본 연구의 구성은 다음과 같다. 1장의 서론에 이어 2장에서는 선행연구를 개관하였다. 촐레스키 분해와 부호제약 방식을 이용한 국내외 선행 논문들과 이들 논문의 분석 결과들을 정리하였다. 3장은 모형 및 연구방법에 대한 설명이다. VAR 모형 분석에서 충격의 식별이 필요한 이유, 부호제약 방식의 방법론 등을 다루었다. 4장은 실증분석 결과이다. 주택시장에 대한 이자율 변동의 동적 파급효과를 충격반응함수와 예측오차분산분해의 결과들을 통해 살펴보았다. 5장은 요약 및 결론이다.

Ⅱ. 선행연구

VAR 모형을 통해 이자율과 주택시장의 관계를 분석한 논문들 중,⁸⁾ 촐레스키 분해를 이용한 연구들로는 해외의 경우 Aoki et al.(2002), Lastrapes (2002), Giuliodori(2005) 등이 있으며, 국내 연구로는 손종칠(2010), 최희갑(2013), 송인호(2015), 엄근용·진창하(2016), 최윤영 외(2017) 등이 있다.

Aoki et al.(2002)은 이자율과 주택가격 그리고 소득 등의 거시경제변수들을 포함하는 VAR 모형을 구축하였으며, 이자율의 순서를 가장 뒤로 위치시키고 있다. 영국의 데이터를 이용한 분석결과는 정책금리 1%p의 상승이 주택가격을 1.6%까지 하락시키는 효과를 갖는다. Giuliodori (2005) 역시 이자율의 위치를 가장 뒤로한 VAR 모형을 분석하였다. 유럽의 9개 국가 모두에서 이자율의 상승은 주택가격을 하락시키는 효과를 가지며, 1%p의 단기금리 상승은 주택가격을 0.6∼1.8% 정도 하락시킨다. Lastrapes(2002)는 주택시장의 변수로서 주택가격 외에 신규주택판매량을 포함하였다. 앞의 두 논문과는 달리 이자율의 위치를 주택시장 변수들보다 앞에 위치시키고 있다. 미국의 데이터를 이용한 분석결과는 0.35∼0.45%p의 단기 금리 상승이 주택가격을 동기에(contemporaneously) 0.1% 하락시키며 최대 0.7%의 하락요인으로 작용한다. 한편, 주택판매량은 동기에 2.5% 하락 그리고 최대 3.5% 하락하면서 단기적인 효과가 주택가격보다 크게 나타나고 있다.

촐레스키 분해를 이용한 국내연구에서 손종칠(2010)과 송인호(2015)는 주택시장과 관련하여 주택가격만을 대상으로 하였으며, 최윤영 외(2017)는 주택가격과 주택거래량을 모두 고려하였다. 손종칠(2010)은 주택가격, 이자율, 거시경제변수들을 포함하는 10변수 VAR 모형을 구축하였다. 촐레스키 분해를 이용한 식별에서 변수의 외생성 추론에 따라 이자율과 주택가격을 중간에 위치시키되 주택가격을 이자율의 앞으로 배치하였다. 콜금리 1표준오차의 상승충격은 최고 0.1%p의 주택가격변동률을 하락시킨다. 송인호(2015)는 이자율-주택가격-인플레이션-총생산의 순으로 변수순서를 배열하였으며, 1.22%p의 콜금리 상승충격은 주택가격변동률을 0.82%p까지 하락시키는 효과를 갖는다. 최윤영 외(2017)는 주택담보대출금리-주택거래량-주택가격-주택소비심리의 순으로 변수순서를 배열하였다. 주택담보대출금리의 상승 충격은 주택가격과 주택거래량 모두를 하락시키는 요인으로 분석되었다.

최희갑(2013), 엄근용·진창하(2016)는 벡터오차수정모형(VECM)에서 촐레스키 분해를 이용하여 충격을 식별하였다. 최희갑(2013)은 이자율, 주택가격, 거시경제변수를 포함하는 8변수 VECM을 설정하고 일반화충격반응함수를 사용하여 충격을 식별하였다.⁹⁾엄근용·진창하(2016)는 이자율, 주택가격 및 전세가격, 통화량, 소득을 포함하는 모형에서 이자율을 가장 앞에 위치시키고 있다. 두 논문 모두 이자율 변수로 CD금리를 사용하였으며, 이자율 상승이 주택가격의 하락요인으로 작용함을 보이고 있다.

부호제약 방식을 이용하여 충격을 식별한 연구로는 해외의 경우 Vargas-Silva(2008), Jarocinski and Smets(2008) 등이 있으며, 국내연구로는 차경수·황상연(2013)과 이근영·김남현(2016)이 있다.

Vargas-Silva(2008)는 이자율 상승충격이 주택가격 및 거시경제변수에 6개월 혹은 12개월 동안 음(−)의 효과를 미친다는 가정을 부호제약으로 이용하였다. 미국의 데이터를 이용한 분석에서 0.25%p의 연방기금금리 상승은 주택가격을 0.6%까지 하락시키는 효과를 갖는다. Jarocinski and Smets(2008)는 동시적 제약과 부호제약을 혼용하여 충격을 식별하였다. 9변수 VAR 모형을 이용한 분석에서 0.25%p의 연방기금금리 상승은 0.5%의 실질주택가격 하락 요인으로 작용하고 있다.

차경수·황상연(2013)은 이자율, 주택가격, 물가, GDP, 통화량의 5변수 VAR 모형에 부호제약 방식을 적용하였다. 분석 결과는 이자율 변동이 주택가격 하락에 유의적인 영향을 미치지 않는 것으로 나타났다. 그러나 이러한 분석 결과는 이자율을 상승시키는 긴축적 통화정책 충격이 주택가격을 제외한 나머지 변수들에서만 음(−)의 충격 효과를 갖는다는 제약 방식과 관련이 있는 것으로 여겨진다. 이근영·김남현(2016)은 이자율, 주택가격, 전세가격의 3변수 모형에 부호제약 방식을 적용하였다. CD 금리 상승은 주택가격 및 전세가격을 하락시키는 효과를 갖고 있으며, 그 효과는 금리 상승기보다는 금리 하락기에 더욱 커진다는 결과를 보고하였다.

Ⅲ. 모형

이자율과 주택시장의 관련성을 살피기 위해 다음과 같은 구조벡터자기회귀(SVAR) 모형을 설정한다.¹⁰⁾

$X_t={\displaystyle \sum _{i=0}^p{A}_i{X}_{t-i}+{\epsilon }_t}$

위 식에서 X_t는 이자율과 주택시장 변수들로 이루어진 k×1 내생변수 벡터이며, A_i는 n×k 계수행렬이다. A₀는 내생변수간의 관련성을 보여주는 계수행렬로써, 대각항이 모두 0인 행렬이다. ε_t는 k×1 충격항 벡터로써 Ω의 공분산행렬을 갖는다. 충격항간의 상관성은 없는 것으로 가정하며, 따라서 Ω의 비대각항은 모두 0이다.

(식 1)은 충격항과 내생변수와의 관계를 나타내는 구조적 모형이다. 그러나 이러한 SVAR 모형은 직접적으로 추정할 수 없으며, 추정이 가능한 축약벡터자기회귀(RVAR) 모형으로 변환하게 된다. 변환된 RVAR 모형은 다음과 같다.

$X_t={\displaystyle \sum _{i=1}^p{B}_i{X}_{t-i}+u_t}$

위 식에서 B_i는 n×k 계수행렬이며, B_i= (I-A₀)^-1A_i이다. 여기서 I는 단위행렬(identity matrix)을 나타낸다. u_t는 k×1 예측오차 벡터로서 Σ의 공분산행렬을 갖는다. u_t와 e_t의 관계는 u_t=(I-A₀)^-1ε_t이며, 계수조정을 통해 다음과 같이 정리할 수 있다.

$u_t=H\times e_t$

위 식에서 H는 k×k 계수행렬로써, e_t의 변화가 초래하는 X_t의 변화 효과-∂X_t/∂e_t-를 나타내는 행렬이다. e_t는 ε_t의 각 항들의 분산을 1로 표준화한 k×1 충격항벡터로써, e_t의 공분산행렬은 단위행렬(I)로 표시된다. e_t의 공분산행렬이 단위행렬이라는 점을 이용하면, (식 3)으로부터의 관계를 도출할 수 있다. H^T는 H의 전치행렬을 표시한다.

${\displaystyle \sum }=H\times H^T$

부호제약에 의한 충격의 식별은 Faust(1998), Canova and De Nicolo(2002), Uhlig(2005), Rubio- Ramirez et al.(2010) 등에 의해 개발된 방법이다. 이 방법은 H를 하나의 정확한 값으로 식별하기보다는 가능한 값들의 집합, 즉 H의 가능한 범위를 찾는데 주안점을 두고 있다. H의 가능한 범위는 (식 4)를 만족시키는 모든 H 중에서, 충격반응함수들의 부호가 선험적 논리에 부합하는 것들로 이루어진다. 부호제약에 의한 여러 가지 식별 방식 중,¹¹⁾ 본 연구에서는 Uhlig (2005)의 방식을 이용하였다.

Uhlig(2005)는 H행렬 전체가 아니라 H행렬의 하나의 열벡터(column vector)에 대한 식별 문제를 다루고 있다. a를 Σ=A×A^T를 만족시키는 행렬 A의 하나의 열벡터라고 하자.¹²⁾ Uhlig는 촐레스키 분해에 의한 하방삼각행렬을 이용하여 a를 다음과 같이 나타낼 수 있음을 보이고 있다.¹³⁾

$a=F\times \alpha$

위 식에서 F는 촐레스키 분해에 의한 하방삼각행렬이며, α는 길이가 1인 단위벡터이다(||α||=1). a는 단위벡터 α의 구체적인 값에 따라 다양한 값을 가지며, 그러한 다양한 값들 중에서 충격반응함수값들의 부호가 선험적 부호에 부합하는 것들을 찾게 된다. 부호제약을 이용한 식별에서는 부호제약기간에 따라 결과가 다르게 나타날 수 있다.

a에 대응하는 충격반응함수 및 예측오차분산분해의 값들은 다음과 같다.¹⁴⁾

$r_a\left(m\right)={\displaystyle \sum _{i=1}^k{\alpha }_i\times r_i\left(m\right)}$

${\Phi }_{a,j}\left(m\right)=\frac{{\displaystyle \sum _{l=1}^m{r}_{a,j}{\left(l\right)}^2}}{{\displaystyle \sum _{l=1}^m{\displaystyle \sum _{i=1}^k\left(r_{i,j}{\left(l\right)}^2\right)}}}$

(식 6)은 충격반응함수(∂X_t+m/∂e_t)를 표시한다. 식에서 r_a(m)은 m시차(horizon)에서의 a에 대응하는 충격반응함수값들(벡터)이며, r_i(m)은 i번째 항의 충격에 따른 촐레스키 분해에서의 충격반응함수벡터이다. α_i는 단위벡터 α의 i번째 원소(element)이다. (식 7)은 m단계 예측오차(m- step ahead forecast error)에 대한 분산분해로서, Φ_a,j는 j변수에 대한 분산분해값을 그리고 r_a,j와 r_i,j는 j변수에 대한 충격반응함수를 표시한다.

Ⅳ. 실증분석

3. 부호제약을 이용한 분석 결과

이자율 상승은 일반적으로 주택가격과 거래량을 위축시키는 효과를 갖는 것으로 알려져 있다. 여기서는 이자율 충격에 의한 이자율 상승이 일정기간동안 주택가격과 거래량을 위축시킬 것이라는 전제를 부호제약으로 이용한다. 이자율 변동이 주택시장에 미치는 동적 효과(dynamic effect)는 충격반응함수와 예측오차 분산분해를 통해 살펴본다.

부호제약은 VAR 변수의 적분(integrated)변수에 대하여 행하였으며,¹⁷⁾ 부호제약기간은 12개월로 설정하였다.¹⁸⁾ (식 6)의 충격반응함수를 계산하기 위한 단위벡터 αi는 일양분포(uniform distribution)에서 추출하였으며, 부호제약을 만족시키는 2,000개의 식별결과를 충격반응함수및 예측오차 분산분해 계산에 이용하였다.

<그림 1>은 부호제약을 이용하여 계산한 2,000개의 충격반응함수의 최소값, 최대값, 그리고 중앙값을 보여준다. 이자율 충격의 크기는 통화정책에서 기준금리 변동이 0.25%p 단위로 이루어지는 점을 감안하여, 0.25%p의 이자율 상승을 초래하는 경우로 조정하였다. 결과를 정리하면 다음과 같다.

그림 1. 이자율 충격(0.25%p)에 따른 충격반응함수 : 부호제약 주 : 점선은 2,000개 시뮬레이션 값의 최소값․최대값이며 실선은 중앙값임.

Download Original Figure

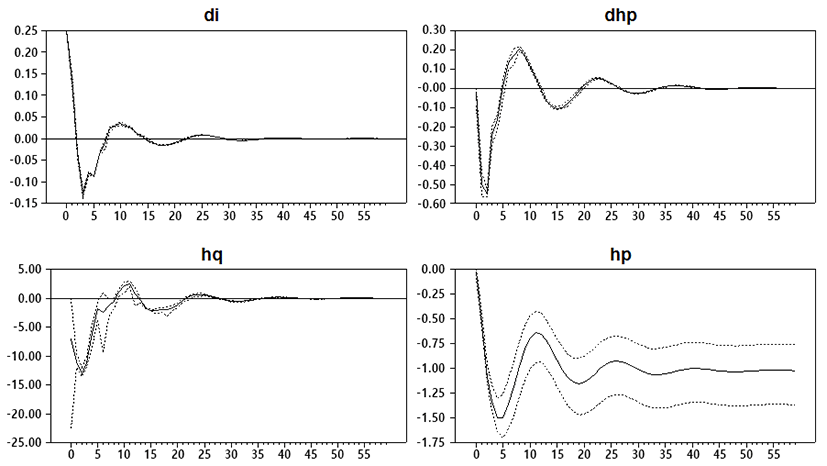
첫째, 이자율 0.25%p의 상승은 동월의 주택가격을 최대 0.09%까지 그리고 동월의 주택거래량을 최대 22.68%까지 하락시키는 효과를 갖는다. 중앙값은 주택가격의 경우 0.03% 하락 그리고 주택거래량의 경우 7.65% 하락하는 것으로 분석된다.¹⁹⁾ 최대값이나 중앙값으로 판단할 때, 이자율 변동의 효과는 주택가격보다는 주택거래량에서 훨씬 크게 나타날 수 있다.

둘째, 이자율 상승의 효과는 거래량 및 주택가격 증가율에서는 2개월 뒤, 그리고 주택가격 수준에서는 4∼5개월 뒤에 가장 극대화되고 있다.²⁰⁾ 이자율 0.25%p 상승 시, 주택거래량은 2개월 뒤 11.90∼13.53% 하락하며, 주택가격 증가율 역시 2개월 뒤 0.52∼0.56%p 하락하는 효과를 갖는다. 주택가격 수준은 4∼5개월 뒤에 1.30∼1.69%까지 하락한다. 이러한 결과는 이자율 변동의 효과가 극대화되는 시점에서의 효과 역시 이자율 변동의 효과는 주택가격보다는 주택거래량에서 훨씬 크게 나타나고 있음을 보여준다.

셋째, 이자율 상승이 주택거래량을 감소시키는 효과는 <그림 1>에서 보는 것처럼 6∼8개월 이후 사라지는 반면, 주택가격의 감소효과는 장기적으로 지속되는 특징을 갖는다. 0.25%p의 이자율 상승에 따른 주택가격의 장기적 하락 폭은 0.77∼1.37% 수준이다.

<표 5>는 예측오차 분산분해결과로서 주택거래량 및 주택가격 증가율 변동에서 이자율 충격의 비중이 얼마나 되는가를 보여준다.

표 5. 예측오차분산분해 : 부호제약

m	최소			최대
	di	dhp	hq	di	dhp	hq
1	89.91	1.14	8.98	99.49	2.29	16.47
2	63.89	15.36	13.76	70.33	17.31	18.93
6	61.67	25.06	20.35	67.86	27.54	22.84
12	58.21	25.94	18.97	63.90	28.46	21.90
36	56.48	26.17	19.14	61.96	28.69	22.00
∞	56.47	26.17	19.14	61.95	28.70	21.42

주 : m은 예측시계(forecasting horizon)를 표시함.

Download Excel Table

장기적으로(예측시계 ∞), 주택가격증가율 변동의 26.2∼28.7%, 그리고 주택거래량 변동의 19.1∼21.4%는 이자율 충격에 따른 효과인 것으로 나타난다. 이자율(주택담보대출금리) 변동에서 주택시장 자체의 충격이 차지하는 장기적 비중은 38.1∼43.5%이다.²¹⁾

4. 촐레스키 분해를 이용한 분석 결과

촐레스키 분해에서는 변수의 순서에 따라 충격의 식별을 위한 기본 전제가 다르게 나타난다. 이자율 변수를 가장 앞으로 놓는 경우(모형 A), 이자율 충격에 따른 이자율 변화는 동 시점에서 주택시장(주택가격과 거래량)에 영향을 미치나 주택시장에서의 충격은 동 시점의 이자율 변화를 초래하지 않는다는 가정을 전제로 하고 있으며, 이자율을 가장 뒤로 놓는 경우(모형 B)에는 주택시장에서의 충격이 동시적인 이자율 변화를 초래하는 반면 이자율 충격은 주택시장에 동시적 영향을 미치지 않는다는 가정이 전제되어 있다.

<표 6>은 모형 A와 모형 B에 대한 H행렬의 식별결과이다. 모형 A에서 첫 번째 열(column)은 이자율 충격에 대한 변수들의 동시적 반응을 보여준다. 식별 결과는 이자율 충격에 의한 이자율 상승이 동 시점에서 주택가격 하락과 주택거래량 감소를 초래하는 것으로 나타나고 있다. 모형 B에서는 마지막 열이 이자율 충격에 대한 변수들의 동시적 반응으로서, 이자율 충격은 주택시장에 동시적 영향을 미치지 않는다.

표 6. H의 식별결과

모형 A: di-dhp-hq $\left(\begin{array}{ccc}0.095& 0& 0\\ -0.046& 0.431& 0\\ -5.097& -0.602& 16.112\end{array}\right)$

모형 B: dhp-hq-di $\left(\begin{array}{ccc}0.433& 0& 0\\ -0.057& 16.910& 0\\ -0.010& -0.0129& 0.090\end{array}\right)$

Download Excel Table

<그림 2>는 촐레스키 분해를 이용하여 구한 이자율 충격(0.25%p)에 따른 충격반응함수이다. 그림에서 실선은 모형 A에서의 그리고 점선은 모형 B에서의 충격반응함수이다. <그림 1>의 충격반응함수와 비교할 때, 모형 B에서의 충격반응함수는 부호제약을 사용하는 경우의 최소값과 유사한 형태를 보이고 있다. 이러한 결과는 촐레스키 분해에서 이자율을 가장 뒤로 배치하는 경우의 동시적 인과관계가 부호제약에서의 최소값이 의미하는 동시적 인과관계와 일치하기 때문에 나타나는 결과이다. 반면에, 모형 A에서의 충격반응함수는 동월의 주택거래량에 미치는 이자율 상승효과에서 큰 차이를 보이고 있으며, 충격반응함수의 형태도 부호제약을 사용하는 경우의 최대값과 다소 차이를 보이고 있다.

그림 2. 이자율 충격(0.25%p)에 따른 충격반응함수 : 촐레스키분해 주 : 실선은 모형 A, 점선은 모형 B의 충격반응함수임.

Download Original Figure

<표 7>에서는 이자율 충격의 효과가 극대화되는 시점과 장기적인 시점에서 촐레스키분해를 이용한 결과와 부호제약을 이용한 결과를 구체적인 수치로써 비교하고 있다. 촐레스키 분해에서의 모형 B의 결과는 부호제약에서의 최소값과 거의 같은 수치를 보이고 있으나, 모형 A의 결과는 부호제약에서의 최대값과 다소 차이를 보이는 것을 알 수 있다. 특기할 만한 것은 모형 A의 결과가 부호제약에서의 최소값과 최대값의 범위를 벗어난다는 점이다.

표 7. 이자율 0.25%p 상승충격의 효과 비교 (단위 : %)

구분	주택거래량	주택가격
(촐레스키 분해)
모형 A	–14.92(2)	–1.83(5)	–1.37(∞)
모형 B	–11.88(2)	–1.30(4)	–0.75(∞)
(부호제약)
최대효과	–13.53(2)	–1.69(5)	–1.36(∞)
최소효과	–11.90(2)	–1.30(4)	–0.76(∞)

주 : ( )안의 수치는 경과개월수를 표시한다.

Download Excel Table

Ⅴ. 요약 및 결과

본 연구에서는 이자율, 주택가격, 주택거래량의 3변수로 구성된 VAR 모형을 사용하여 이자율 변동이 주택시장에 미치는 영향을 분석하였다. 이자율은 주택담보대출금리, 주택가격과 주택거래량은 아파트실거래가지수와 아파트매매거래량을 사용하였으며, 데이터 기간은 2008년 1월부터 2017년 6월까지이다.

이자율 충격의 식별은 부호제약 방식을 이용하였다. 분석결과는 다음과 같다. 첫째, 이자율 충격의 효과가 극대화되는 시점은 주택거래량에서는 2개월 뒤, 주택가격에서는 4∼5개월 뒤이다. 둘째, 주택대출금리가 0.25%p 상승하는 경우, 주택거래량은 11.9∼13.5%까지 감소하며, 주택가격은 1.3∼1.7%까지 하락한다. 셋째, 주택대출금리가 0.25%p 상승하는 경우, 주택거래량 감소효과는 6∼8개월 이후 사라지는 반면 주택가격 감소효과는 사라지지 않는다. 주택가격의 장기적 하락 폭은 0.8∼1.4% 수준이다. 넷째, 장기적으로 주택가격변동의 26.2∼28.7% 그리고 주택거래량변동의 19.1∼21.4%는 이자율 충격에 의해 발생한다.

연구의 시사점은 두 가지 측면에서 살펴볼 수 있다. 먼저 연구결과 측면에서의 시사점이다. 본 연구의 분석결과에 의하면, 이자율 변동이 미치는 효과는 주택가격보다 주택거래량에서 압도적으로 크게 나타나고 있다. 또한 주택가격이나 주택거래량의 변동에서 이자율 충격이 차지하는 비중도 20%를 웃도는 높은 수준이다. 이자율 변동의 결정적 요인은 통화정책이다. 통화정책 수립 과정에서 이자율이 주택시장에 미치는 이러한 효과들을 충분히 고려하여 정책 결정을 내릴 필요가 있을 것이다.

두 번째는 방법론 측면에서의 시사점이다. 통상적으로 사용되는 촐레스키 분해에서는 변수의 배열순서 즉, 동시적 인과관계에 대한 순서가 가정되어 있으며, 변수의 배열 순서에 따라 결과도 달라진다. 그러나 동시적 인과관계 순서의 적정성에 대한 실증적 검증은 매우 어려운 작업이며, 본 연구에서 살펴본 것처럼 분석결과가 부호제약 방식을 사용한 분석결과의 범위를 넘어서기도 한다. 부호제약 방식에서의 기본 가정이 보다 현실적인 가정이라는 점을 감안하면, 다소 무리한 0의 제약을 사용하는 여러 가지 식별방식에 의한 분석보다는 부호제약을 이용한 분석결과가 선호될 수 있을 것으로 생각된다.

본 연구의 분석결과는 3변수 VAR 모형에 기반하고 있다. 향후 이자율 변수를 정책(기본)금리와 주택대출금리로 구분하고, 주택대출액 등 통화정책의 신용경로를 반영할 수 있는 변수를 모형 내에 도입한다면, 보다 정치한 결과가 도출될 수 있으리라 기대한다.