Ⅰ. 서론
2006년 1월 실거래가 신고제도가 시행되고 실거래가를 이용한 많은 연구가 진행되어 왔다. 국토교통부의 경우, 2009년 12월부터 반복매매모형을 이용하여 2006년 1월을 기준으로 하여 아파트 실거래 가격지수를 발표하고 있다. 두 번 이상 거래된 자료를 바탕으로 지수를 산정하는 반복매매 지수는 Bailey et al.(1963)을 시작으로 Case and Shiller(1987), Goetzmann(1992), Shiller(1991) 등에 의해 발전되어 왔다. 우리나라는 실거래가 신고제도가 시행되기 이전에는 매매 시세 자료를 통해 아파트 가격지수와 월세지수를 산정하기 위해 반복매매모형을 활용한 사례가 있다(이창무 외 2002; 외 2003). 실거래가 신고제도가 시행된 이후에는 실거래가를 이용한 반복매매지수가 만들어졌다(이창무 외 2007).
많은 시간과 비용이 드는 헤도닉 가격지수나 SPAR 지수와는 달리, 반복매매지수는 반복으로 거래된 주택 거래 시점과 가격만 있으면 지수를 산출할 수 있다(류강민·이창무 2011). 하지만 반복매매지수는 실거래가 자료 중 반복으로 거래된 자료만을 이용하기 때문에 자료의 비효율성 문제가 항상 대두된다. 또한 새롭게 발생한 거래건이 과거 이용되지 않았던 거래건과 거래쌍을 구성하여 활용됨으로 인해 과거 지수값이 변화한다는 문제가 발생한다(류강민 외, 2009; 이창무·배익민, 2008; Case and Shiller, 1987; Goetzmann, 1992; Goetzmann and Peng, 2002; Peng, 2002; Shiller, 1991).
2006년 1월 실거래가 신고제도가 시행된 이후 반복매매지수가 많이 이용되고 있지만, 여전히 해결해야 할 주요한 문제점이 존재한다. 그 중 가장 중요한 문제점은 자료의 이용효율이 낮아 거래수가 부족한 하부시장에서 지수산정이 극히 불안해진다는 점이다. 가장 거래가 많은 서울시 아파트시장의 경우도 자치구 단위로 지수를 산정하지 못하고, 5개 권역으로 나누어 월지수를 산정하고 있을 뿐이다. 그 중 도심권역은 종로구, 중구, 용산구의 3개구를 포함하고 있음에도 불구하고, 거래량이 충분치 못해 지수의 안정성이 보장되지 못하고 있다. 이와 같이 거래량이 충분치 않은 하부시장의 가격지수를 산출하기 위한 지수산정방법으로 이동평균지수나 MIT/CRE 지수 적용이 가능하나, 이 또한 그리 만족스럽지 못한 것이 현실이다.
서울시 전체 혹은 생활권역별 가격지수는 아파트를 매매하는데 있어 지역의 범위가 매우 넓기 때문에 매매하고자 하는 지역의 실제 매매가격 변동률은 완전하게 보여주지 못한다는 한계점이 있다. 분양가 상한제 적용지역이 동 단위로 발표된 이후 사람들이 권역별이 아닌 자치구 및 동단위 가격 변동 추이에 관심을 더 많은 관심을 보이고 있어 보다 세분화된 하위시장 지수에 대한 요구가 증가하고 있다.
따라서 본 연구에서는 거래량이 적은 아파트의 지역별 하위시장에서 안정적인 지수를 산출하기 위한 방법으로 해당 월과 이전 월의 자료를 중첩하여 해당 월 자료로 이용하여 지수를 산출하는 방식으로 단순하지만, 안정적인 지수의 산출이 가능한 중첩 모형을 제안하고자 한다. 중첩 반복매매모형은 S&P/Case-Shiller Home Price Index 산정에 이용되고 있는 방식(S&P Dow Jones Indices, 2020)으로 기존의 방법론과 모형을 달리하여 ‘smoothing’ 기법을 적용하는 것이 아닌 이용 자료를 다루는 방식을 보완한 것이다. 이러한 방식은 거래자료 수가 부족하여 지수를 안정화하고자 할 때 어떤 모형을 활용하더라도 언제든지 적용하여 지수 성능을 개선시킬 수 있다는 장점이 있다.
중첩 모형의 추정 성능을 평가하기 위해 비교 대상으로는 동일가중 기하평균 반복매매지수와 3개월 이동평균지수, MIT/CRE 지수를 산출하고, 통계적 신뢰도, 지수의 안정성, 지수변화(revision)의 측면에서 비교 평가한다.
Ⅱ. 선행연구 고찰
이창무 외(2002)는 주택시장의 가격지수로서 반복매매모형에 기반을 둔 지수산정방식을 제안하고 그 특성에 대하여 논의하였다. 이에 한국의 부동산 가격자료가 시세자료에 의존했던 상황을 고려한다면, 헤도닉 모형에 바탕을 둔 지수의 산정방법에는 현실적인 한계가 존재한다. 하지만 반복매매모형은 시세조사자료의 특성과 부합하는 구조를 지니고 있으며, 더 나아가 희소한 반복거래사례에 바탕을 둔 반복매매모형이 지닌 자료이용의 비효율성과 표본추출편의(sampling bias)의 문제, 반복거래 관측기간의 증가에 따른 이분산성의 문제를 극복하고, 자료구조의 단순성이라는 반복매매모형의 장점만을 취할 수 있는 구조를 지니고 있다고 하였다.
이창무 외(2005)는 시장에서 관측될 수 있는 실거래자료를 이용하여 기존 시세지수의 한계를 극복할 수 있는 실거래가지수 산정방식을 개발하고, 제안된 실거래가지수가 지닌 성격을 기존에 발표되어 오던 시세지수와의 관계를 통해 살펴보았다. 종합주가지수방식의 지수산정모형은 고정된 스톡의 총자산가치의 상대적인 변동을 측정하여 지수를 산정하는 것으로서, 지수산정식이 매우 간단하고 하부주택시장의 지수산정이 용이하다는 장점이 있지만, 신규주택의 공급과 기존주택의 멸실과 같은 스톡의 변화를 제대로 반영하기 어렵다는 한계가 있다고 보았고, 헤도닉 모형을 이용한 주택가격지수의 산정은 이론적으로는 가능한 대안이나 최적모형이 시간에 따라 변할 수 있다는 점과 방대한 주택특성자료를 시계열적으로 구축해야 한다는 점을 고려할 때, 현실적으로 적용하기 어려운 모형이라 보았다. 이에 비해 반복매매모형의 경우, 동일단지, 동일평형의 모든 아파트가 동일한 주택이라는 가정 하에서 단지 동일한 주택의 2개 시점의 가격자료만으로 지수를 산정할 수 있고, 주택특성을 따로 통제할 필요도 없으므로, 신거래가지수의 산정에 있어서는 가장 적적할 대안이라 보았다.
이창무 외(2007)는 반복매매지수모형이 지수산정기간 내에 두 번 이상 거래된 주택의 자료만을 사용하게 되는 자료이용의 비효율성이란 문제를 국내의 아파트시장을 대상으로 동일단지, 동일평형을 동일주택으로 가정한 반복매매지수를 산출하여 하부시장의 구분에 따른 반복매매지수의 통계적인 적합성을 검증하였다. 연구결과, 반복매매지수모형은 입지특성의 변화에 따른 가격변동분을 포함하는 지수를 산출하는 반면, 시변계수 헤도닉지수모형은 입지특성의 변화에 따른 가격변동분이 누락된 지수를 산출함을 보여주며, 이에 따라 장기적인 도시성장과정에서 요구되는 가격지수는 주택의 구조적 특성에 대한 통제가 적절히 이루어진다면 반복매매지수모형이 더 적합한 선택이 될 수 있다 주장하였다.
이창무·배익민(2008)은 실거래가를 이용한 반복매매지수가 가지는 비효율성의 문제를 부분적으로 극복하기 위해 시세자료를 활용하여 반복매매지수의 효율성을 향상시킬 수 있는 방법론을 제안하였다. 연구결과, 시세가격을 반복매매모형에 작용함에 따라 자료사용의 효율성이 향상되고, 지수변동성의 크기도 큰 폭으로 감소하는 등 긍정적인 효과를 나타냈지만, 시세가격은 신규주택들에 대한 고려를 못한다는 점과 실거래가격과 본질적인 차이가 있다는 한계점이 있었다.
류강민·송기욱(2020), 황규완·손재영(2017)은 반복매매모형 등 기존의 가격지수 산출기법을 활용하기 어려울 정도로 부족한 거래 자료를 바탕으로 분기별 가격지수를 산출하였다. 이를 위해 서울 오피스 매매사례 자료를 기반으로 MIT/CRE (Massachusetts Institute of Technology/ Center for Real Estate)에서 개발한 2단계 추정법을 활용해 서울 오피스 매매가격 지수를 산출했다. 기존의 반복매매모형을 이용하여 연지수를 우선적으로 산출하는 1단계 과정에서 각각 Baily et al.(1963)의 동일가중-기하평균 반복매매모형과 Shiller(1991)의 가치가중-산술평균 반복매매모형을 활용하였다는 점에서는 차이가 있으나, 이용할 수 있는 매매사례 자료가 제한적임에도 불구하고, 모든 분석기간에 대해 반복 거래쌍을 확보하여 보다 신뢰성 있는 안정적인 서울 오피스 실거래가격지수를 산출할 수 있었다.
과거 실거래가 신고제도의 도입과 함께 실거래가 자료에 기반한 가격지수 산정방식에 관한 연구가 꾸준히 진행되어져 왔고, 그 방법론으로서 반복매매모형이 자리 잡았다. 이창무·배익민(2008)은 시세자료를 실거래가 자료와 함께 활용하는 방안을 제시하였고, 류강민·송기욱(2020), 황규완(2017), 황규완·손재영(2017)은 2단계로 구성된 모형을 활용함으로써 반복매매모형이 기본적으로 가지는 자료 이용의 비효율성을 해결하고자 하였다. 그러나 시세자료는 기본적으로 조사된 가격으로 실거래가 자료와 본질적인 차이가 있고, 신규주택 혹은 멸실에 대한 반영이 늦다는 한계점이 있다. 또한 MIT/CRE 2단계 추정법의 경우에는 모형의 특성으로 인해 실제 시장의 가격변동 추이와 1~2분기 정도의 시차가 발생하여 시장 상황을 빠르게 보여 적시성의 측면에서 한계가 있다.
본 연구에서는 거례사례가 부족한 한계점을 극복하기 위한 방안인 중첩지수를 2006년 1월부터 2019년 8월까지의 아파트 실거래가 자료를 바탕으로 반복매매모형을 활용하여 가장 기본적인 동일가중-기하평균 모형, 이를 활용한 3개월 이동평균지수 그리고 자료수 부족으로 안정적인 지수산정에 어려움이 있는 오피스 시장에 대하여 민간(이지스자산운용·대신증권, 2019)에서 적용하고 있는 MIT/CRE 2단계 추정법을 통한 지수를 산출하여 비교, 분석하였다.
Ⅲ. 분석 방법
반복매매지수는 Bailey et al.(1963)에 의해 처음 제시한 모형으로 지수 산정비용이 적고, 실거래가격에 기초하여 시장 변화를 즉각적으로 반영하는 지수 산정이 가능하다. 반복 거래된 부동산의 가격을 이용하기 때문에 헤도닉 가격지수와 같이 방대한 부동산 특성자료들이 불필요하고, 두 번 이상 거래된 건물의 실거래가격만 있으면 지수를 만들 수 있는 장점이 있다. 하지만 반복매매 거래쌍을 구성하기 위해서 관측되는 실거래가 자료수가 적어 안정적인 지수 산정에 한계가 있다. Bailey et al.(1963)의 지수산정 모형은 반복매매모형의 가장 기본적인 형태로 본 논문에서는 ‘일반 반복매매모형’으로 기술하기로 한다.
2회 이상 거래된 주택을 대상으로 첫 번째 거래와 두 번째 거래 시점의 가격 정보를 이용해 지수를 산정하는 반복매매지수 산정식은 다음의 (식 1)과 같다. 먼저, 부동산 i의 첫 번째 거래가격(Pif)과 두 번째 거래가격(Pis)의 가격비율에 자연로그를 취한 값 ln(Ps/Pf)을 종속변수로 하고, 처음 거래 시점 f와 다음 거래 시점 s을 표현하는 더미변수 Dt를 도입하여 설정된다.
여기서 Dt는 t시점이 두 번째 거래시점(s)인 경우 1, 첫 번째 거래시점(f)인 경우 –1, 그 외에는 0의 값을 가지게 된다. 이러한 방식으로 매 시점의 누적가격변동률 βt가 산출되면 t시점의 지수는 (식 2)와 같이 산정된다.
3개월 이동평균 지수는 지수 값의 상하 변동폭을 안정화시키기 위한 방식으로, 산출된 일반 반복매매지수의 3개월 지수 값의 평균으로 구한다. 일반 반복매매지수의 평균값을 이용하므로 일반 반복매매지수에 비해 변동성이 적어지는 특성을 지닌다. 기본적인 지수 값()은 (식 1), (식 2)을 통해 일반 반복매매지수를 산정한 후, (식 3)과 같이 이전 두 달과 해당 달의 산출된 지수 값의 평균을 해당 시점 지수로 정한다.
3개월 중첩 지수는 분석에 사용되는 표본으로 해당 당월과 그 이전 두 개 시점의 자료를 중첩하여 이용하며, 지수를 안정화시키는 방식이다. 기본적인 지수 산정 모형은 (식 1), (식 2)의 일반 반복매매모형과 동일하지만, 지수 안정화를 위해 이전 2개월의 자료 ()를 해당 월 자료 ()에 병합하여 해당 월의 새로운 자료()를 구축한다.
이러한 자료 활용방식은 연결된 두 기간의 자료가 중첩되어 이용됨으로써 각 시점의 지수값이 독립적이지 않고 이전 지수 수준에 제약되어 변화하는 구조를 만들어낸다. 이를 통해 각 시점의 지수값이 독립적으로 산출되어 자료수가 부족한 경우 지수산정이 안정적이지 못한 한계를 보완한다. 또한 불안정한 일반 반복매매지수의 2개월 이동평균 방식은 산정된 모든 월 지수가 동일한 영향력을 미치는 반면, 중첩지수는 해당 월과 이전 2개월의 자료를 병합하여 활용하는 관계로 자료수가 많은 월의 가중치가 크게, 상대적으로 자료수가 적은 월의 영향력이 작게 반복매매지수의 산정 시 직접 조정된다.
MIT/CRE 2단계 추정법은 자료수 부족의 문제를 해결하기 위해 MIT 부동산 연구센터에서 개발되었으며(Geltner and Bokhari, 2008), 미국의 상업용 부동산 전문기업인 RCA(Real Capital Analytics)에서 과거에 발표하였던 상업용 부동산 가격지수 Moody’s/REAL CPPI, Moody’s /RCA CPPI를 산정하는 데 활용하였던 방법이다. 분기 단위 지수 산정을 위해 첫 번째 단계로 한 개 분기씩 미뤄진 4종류의 연지수 set를 구성하여 기존의 반복매매모형을 통해 연 증감률 4개 set를 산출하고, 이를 바탕으로 Moore-Penrose의 의사역행력을 이용하여 분기 단위 가격변동률을 산출하는 방식이다.
기존의 관련 선행 연구에서는 연지수 set를 통해 최종적으로 분기 가격변동률을 재구성하는 방식이었다면(류강민·송기욱, 2020; 황규완·손재영, 2017), 본 연구에서는 목적상 한 개월씩 미뤄진 3종류의 분기가격변동률(rA~rC) set를 구성하고, 이를 통해 월 가격변동률(r1~rt)을 재구성하는 방식을 채택하였다.
1단계에서는 2006년 1월~2006년 3월을 첫 번째 분기로 하는 set A, 2006년 2월~2006년 4월을 첫 번째 분기로 하는 set B, 2006년 3월~2006년 5월을 첫 번째 분기로 하는 set C를 각각 구성하여 각각의 set별로 일반 반복매매모형을 이용하여 3개의 분기지수를 산출한다. 이 과정에서 자료가 적은 월의 자료는 분기단위 자료의 일부분이기 때문에 분기지수 산정 시에는 자료부족에 따라 발생할 수 있는 문제를 1차적으로 줄일 수 있다.
이러한 방식으로 산출되는 각 set별로 매 연도의 n번째 분기 가격변동률은 다음의 (식 5)와 같이 나타낼 수 있다.
2단계에서는 (식 5)의 연립방정식을 이용하여 월 가격변동률을 추정한다. 다만, 3개의 식을 통해 추정해야 하는 월 가격변동률 변수는 5개이기 때문에 여러 개의 해가 존재할 수 있어 Moore-Penrose의 의사역행렬(pseudoinverse)를 이용하여 한 개의 해를 구할 수 있다.
이러한 방식으로 부족한 자료수의 영향을 덜 받을 수 있는 분기지수를 우선적으로 산정한 후 이를 이용하게 되면 최종적으로 산출되는 월 가격변동률 또한 자료수 부족으로 인한 영향을 덜 받게 되어 보다 안정적인 월지수의 산정이 가능하게 된다.
그러나 MIT/CRE 지수 산정 시 각 분기지수 set별로 n개 시점에 대해 n- 1개의 분기 변동률을 산출하고, 이를 통해 월 변동률을 산출함으로써 최종적으로는 총 3n개 시점의 자료를 통해 3n-3개의 변동률을 산출하게 되어 초기 3개 시점의 월 변동률 산출에 어려움이 있다는 한계점이 존재한다.
지수의 성능을 평가하는 지표는 몇 가지가 있는데, 그 중 지수의 통계적인 신뢰도를 나타내는 가장 기초적인 평가지표는 추정치의 표준오차이다. 다만, 추정치의 단위나 수준이 다른 경우 표준오차 값이 큰 차이를 보이므로 많은 경우 추정치의 평균적인 수준을 통제하고 단위에 영향을 받지 않는 평가지표로서 변이계수(CV= standard deviation/mean)가 주로 이용된다. 그러나 가격지수의 경우 지수 값이 절대적인 수준이 아니라, 기준시점 대비 누적가격변동률의 성격을 지닌 상대적인 값으로 기준 시점을 다르게 설정할 경우 지수 값이 달라지는 특성이 있어 동일한 표준오차를 가진 지수의 기준시점을 변경할 경우 지수 값의 수준이 함께 변하게 되어 지수 값의 수준이 커질수록 변이계수가 감소하는 문제점이 발생할 수 있다(이창무 외, 2013). 따라서 4가지 모형의 지수화 된 표준오차의 평균값(Mean of Standard Error of Index, MSEI)으로 그 통계적 신뢰도를 평가하기로 하며, (식 6)과 같이 산출할 수 있다.
다만 MIT/CRE 지수는 기본적으로 under-determined된 연립방정식을 전제로 하므로 최소자승법을 적용해 추정된 값은 모두 R2=1.00이기 때문에 t 통계량, 표준오차 등을 산출할 수 없거나 의미를 부하기 어렵다(황규완·손재영, 2017). 또한 2개월 이동평균지수 역시 기본적으로 반복매매지수 값에서 이전 달과 해당 달의 산출된 지수 값의 평균으로 산정되기 때문에 표준오차 등을 산출하는데 한계가 있다. 따라서 본 연구에서 모형별 통계적 신뢰도 평가비교는 제한적으로 동일가중 반복매매지수와 중첩지수간의 비교를 통해서 진행하였다.
이창무 외(2013)는 지수 추세의 안정성을 평가하는 안정성 지수(Stability Index, SI)를 개발하였다. 기본적인 개념은 지수의 초기 시점과 마지막 시점 간 직선거리 대비 지수 그래프의 총 길이의 비를 통해 나타낸다. 따라서 지수값들이 연속적으로 초기지수와 마지막 시점 지수점을 연결하는 선상에 놓이면 1이 되고, 그 직선 상에서 많이 벗어나 위치할수록 0쪽으로 작은 값이 산출된다.
기준 시점이 1, 마지막 시점이 T이고, t시점의 지수 값을 It라고 할 때, 안정성 지수 SI는 다음과 같은 (식 7)을 통해 산정된다.
SI는 0에서 1 사이의 값을 지니며, 안정적일수록 커지며 1에 가까워진다. 따라서, SI 값이 클수록 보다 안정적인 지수로 평가할 수 있으나 그 값이 일정 수준 이상으로 크게 나타날 경우, 지나치게 평활화 되었다는 것을 의미하기도 하므로 SI 지표를 이용하여 지수 산정 모형을 비교함에 있어서 해석에 주의를 할 필요가 있다.
지수 변화(revision)는 매 시점에 새로 산정된 지수의 과거시점의 지수가 변화하는 것으로, 반복매매모형의 특성상 자료가 추가됨에 따라 기존에 지수 산정에 이용되지 않았던 과거의 거래자료가 새로이 반복 거래쌍을 형성하게 됨으로써 나타나는 변화를 나타낸다.
새로 산정된 지수에서 Revision이 발생하더라도 이는 더 많은 자료가 이용됨으로써 발생하는 것으로 어느 정도 수준에서 지수변화의 발생을 허용하는 것이 바람직할 수 있으나, 그 변화 정도가 크게 나타날 경우 시장에는 큰 혼란을 야기할 수 있는 문제가 있다. 따라서 지수 산정 모형별로 발생하게 되는 지수 변화의 정도를 RI(Revision Index)로 지표화하여 지수 성능을 비교하기로 한다.
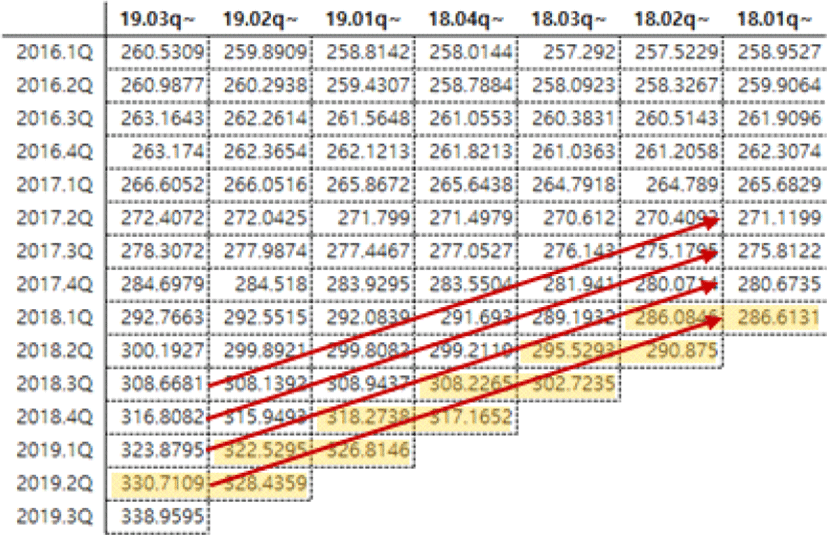
<표 1>에서 0시점은 현재 시점을 나타내고, −1시점은 현재시점에서 한 시점 전의 시점을 나타낸다. 그리고 세로축은 지수산정 시점을, 가로축은 산정된 지수에서 어느 시점의 지수 값인지를 나타낸 것으로 현재 시점이 2019년 8월 말이라고 하면, P00은 2019년 8월 말에 산정된 지수의 2019년 8월 지수 값이며, P01은 2019년 8월 말에 산정한 2019년 7월 지수를 나타내고, 마찬가지로 P11은 2019년 7월말에 산정된 지수의 2019년 7월 지수를 나타낸다. 여기서 지수변화 지표 RI는 2019년 7월 말에 산정된 2019년 7월 지수가 2019년 8월 말에 새로 산정되면서 얼마나 변화했는지를 나타내는 것으로 P01과 P11를 계산하게 되며, 이러한 변화들을 나열하였을 때 얼마나 과거(s)에 산정된 지수까지를 살펴볼 것인지, 각 시점별 산정된 지수 중 몇 기간(n) 이전의 지수까지를 비교할 것인지를 선택하여 각각의 지수변화 정도를 평균하여 아래의 (식 8)과 같이 계산할 수 있다.
| 지수 산정 시점 | 지수 시점 | ||||||
|---|---|---|---|---|---|---|---|
| 0 | -1 | -2 | -3 | -4 | -5 | -6 | |
| 0 | P00 | P01 | P02 | P03 | P04 | P05 | P06 |
| -1 | P11 | P12 | P13 | P14 | P15 | P16 | |
| -2 | P22 | P23 | P24 | P25 | P26 | ||
| -3 | P33 | P34 | P35 | P36 | |||
| -4 | P44 | P45 | P46 | ||||
| -5 | P55 | P56 | |||||
| -6 | P66 | ||||||
<그림 1>을 예로 들면, 2019년 3분기에 산정된 지수부터 2018년 1분기에 산정된 지수까지를 이용하여 노란색 박스 안의 두 지수값의 차이를 산출하기 때문에 s는 6이고(노란색 박스 6개), 산정된 지수에서 최근시점부터 4개 시점 이전까지의 지수 값을 비교하기 때문에 n은 4가 된다(빨간색 화살표 4개).
본 연구에서는 이와 같은 방식으로 시점별 Revision을 구한 후, 시점을 한 시점씩 줄여가면서 16개 시점의 Revision 변동치의 평균을 구하여 각 모형의 RI를 산출하였고, 각각의 RI 값을 통해서 각기 다른 산정방법에 따른 지수들의 Revision을 비교하였다. 다만, 각기 다른 모형의 Revision을 비교함에 있어 지수 값의 수준 차이가 RI 값의 수준에 영향을 줄 수 있기 때문에, 매월 지수 값 대신 가격변동률을 이용하여 Revision을 살펴보았다.
Ⅳ. 분석 자료 및 실증분석 결과
본 연구에 사용한 자료는 국토교통부 실거래가 신고 자료로 분석의 시간 범위는 실거래가 신고가 의무화 된 2006년 1월부터 2019년 8월까지이다. 자료수가 적어 안정적인 지수 산정에 한계가 있는 자치구별 하위시장 지수를 산정하고자 하였다. 2006년 1월부터 2019년 8월까지 서울시 전체 995,292건의 실거래 신고자료 중 자치구별 누적 신고자료 수는 아래 <그림 2>와 같이 나타났는데, 이 중 각각 7,213건, 9,779건으로 가장 적은 자료 수를 포함하고 있는 종로구, 중구와 아파트 시장에서 주요 관심 대상이 되어온 지역으로 63,751건의 자료를 포함하고 있는 강남구를 공간 범위로 설정하였다.
이창무·류강민(2011)에서 살펴본 바와 같이, 반복매매모형은 거래 쌍의 관측빈도가 낮아 자료이용의 비효율성이 가장 큰 문제로 거론된다. 이에 대한 대안으로 유사한 특성을 가진 주택의 동일주택 가정을 통하여 반복거래 쌍을 구성하는 방법이 사용되고 있다. 본 연구에서도 동일주택 가정을 고려하여 표본별로 (법정동+본번+부번+층 그룹+규모 그룹)을 동일주택으로 가정하여 지수를 산정하였다. 층 그룹은 1~2층을 저층 그룹으로 구성하고, 나머지 층을 그룹으로 구성하였으며, 면적 규모는 한국감정원 전국주택가격 동향조사 산정방식을 참고하여 <표 2>와 같이 6개 그룹으로 구성하였다.
| 아파트 | |
|---|---|
| 규모1 | 40m2 이하 |
| 규모2 | 40m2 초과~60m2 이하 |
| 규모3 | 60m2 초과~85m2 이하 |
| 규모4 | 85m2 초과~102m2 이하 |
| 규모5 | 102m2 초과~135m2 이하 |
| 규모6 | 135m2 초과 |
거래자료 중에는 신고상 오류로 인해 가격 혹은 면적이 잘못 기입되어 있는 경우, 특정 거래유형으로 시장의 거래가격과 큰 차이가 있는 경우 등 이상치가 존재할 수 있는데, 이러한 이상치의 존재는 안정적인 지수 산정을 방해하는 요소가 될 수 있다. 따라서 단위가격을 기준으로 하여 Box-plot을 이용하여 이상치 제거 과정을 수행하였다.
그러나 시점별·자치구별로 가격 수준의 이상치를 검출함에 있어 매 시점별로 가격의 편차가 크게 차이날 수 있고, 실제로 가격이 크게 하락 또는 상승한 특정 시점의 경우, 상당수의 거래가 이상치로 판별될 수 있다. 특히 거래자료 수가 부족한 경우에는 이상치 판별 기준 선택을 위해 이용하는 중위값, 사분위수 등의 산출에 있어 이러한 문제들이 보다 크게 나타날 수 있기 때문에 중위값은 과거 1년치, 사분범위(IQR)는 과거 4개월치의 자료를 묶은(pooling) 자료를 이용하여 이상치 판단 기준을 산출하였다. 또한 Box-plot을 이용할 경우 낮은 가격에 비해 높은 가격이 분기별 대푯값이 되는 중위값으로부터 멀리 떨어져 있는 비대칭 분포의 문제가 있어 단위 거래가격을 log 변환한 값을 이용하였다. 이러한 방식으로 최종적으로는 [제1사분위수-1.5IQR], [제3사분위수+1.5 IQR]을 이상치 판단 기준으로 삼았다.
그 결과, 강남구 35건(0.1%), 종로구 161건(2.2%), 중구 125건(1.3%)의 자료가 이상치로 분류되어 제거하였다.
<그림 3>은 자치구별, 연도별 이용자료 수를 나타낸 것으로 강남구와 비교하여 종로구, 중구의 거래자료 수가 상당히 적을 것을 확인할 수 있다. 연도별로는 2006년, 2015~2018년에 3개 자치구 모두에서 거래가 많이 발생한 것으로 나타났고, 2019년의 경우에는 8월까지 만을 포함하고 있어 다른 연도와 직접적으로 비교하기에는 무리가 있다. 월별 이용자료 수를 살펴보면 강남구, 종로구, 중구에서 각각 월 평균 386, 43, 59건의 자료가 이용되었음을 확인할 수 있었다.
<표 3>은 이상치 제거 후 지수산정에 이용되는 거래자료에 대한 기초통계를 나타낸 것이다. 강남구, 종로구, 중구에 대하여 각각 63,716, 7,052, 9,654건의 자료가 이용되었고 거래된 아파트 규모 평균은 전용면적 80m2 내외로 나타났다. 평균 거래가격에 있어서는 강남구가 1,186만 원/m2로 각각 592만 원/m2, 647만 원/m2로 나타난 종로구, 중구에 비해 2배 가까이 높은 거래가격을 나타내고 있었다.
반복매매지수 산정을 위해 앞서 선택한 [읍면동+본번+부번+층그룹+면적그룹]의 동일주택 가정을 기준으로 하여 반복 거래쌍을 구성한 결과, 분석기간 내 2회 이상 거래되어 거래쌍을 구성해 최종적으로 지수산정에 이용된 자료 수는 강남구 63,292건, 종로구 6,974건, 중구 9,561건으로 각각 원자료와 비교하여 99.3%, 96.7%, 97.8%의 자료 이용률을 나타내었다.
<그림 4>, <그림 5>, <그림 6>와 같이 강남구, 종로구와 중구 각각에 대하여 아파트 매매 실거래자료를 이용하여 일반 반복매매지수, 3개월 이동평균 지구, 중첩지수, MIT/CRE 지수를 산정하여 비교하였다. 앞서 이동평균 지수와 중첩지수의 경우 2개월을 기준으로 하였으나, MIT/CRE 지수 산출 시 3개월의 자료를 병합하여 분기지수를 우선적으로 산출하고, 이를 통해 월 변동률을 최종적으로 산출하기 때문에 직접적인 비교를 위해 이동평균 지수와 중첩지수 모두 3개월을 기준으로 하였다.
또한, MIT/CRE 지수 산정 시 초기 3개 시점의 월 변동률 산출에 어려움이 있고, 중첩 지수의 경우에도 처음 두 개 시점에서는 3개월치 자료가 중첩이 되지 않아 이용 자료수 부족으로 인해 초기시점에 상대적으로 불안정한 결과가 산출될 수 있어 지수의 기준시점은 2006년 4월로 하였다.
기본적으로 모형별 지수의 추이는 유사하게 나타났으나, 3개 자치구 모두에서 일반반복매매지수가 불안정하게 나타난 반면에, 나머지 세 종류의 지수는 비교적 안정적으로 나타난 것을 확인할 수 있다. 다만, 강남구의 경우 종로구, 중구와 비교하여 6배 이상의 자료 수가 이용되어 일반 반복매매지수의 불안정한 정도가 크게 나타나지는 않았고, 월 평균 이용자료 수가 43건으로 가장 적은 자료가 이용되는 종로구에서 일반 반복매매지수가 가장 불안정하게 나타났다. 이는 월별 가격변동률을 나타내는 막대그래프에서도 확인할 수 있는데, 일부 구간을 제외하면 대체적으로 일반 반복매매지수를 통해 산출된 월 가격변동 폭이 크게 나타났다.
그 외에 지수산정 모형별로 지수 값의 수준에 차이가 나는 것을 확인할 수 있는데, 이는 자료 수가 부족한 경우 초기 시점의 가격변동률이 불안정하게 나타나기 때문에 지수의 기준 시점을 어느 시점으로 하는 지에 따라 나타나는 차이로 볼 수 있다. 또한 MIT/CRE 지수의 경우, 1개월씩 미뤄진 3개의 분기지수 set를 이용하여 월 변동률을 산출하는 두 번의 과정을 거치는 모형 특성상 지수의 상승·하락 추세가 변하는 극점을 기준으로 봤을 때 약 1개 분기 정도의 시차가 발생하는 것을 확인할 수 있다.
그래프만을 살펴봤을 때 일반 반복매매지수에 비해 나머지 방법론을 통해 산정된 지수가 더 안정적이라는 점, 그리고 중첩 지수, MIT/CRE 지수에 비해서 2개월 이동평균 지수가 조금 더 불안정한 지수 형태를 나타내고 있다는 점 외에는 그래프의 형태만으로는 각 모형별 지수의 추정 성능에 대한 비교에 한계가 있어 구체적인 지수 평가 지표를 통해 비교해 보기로 한다.
모형별 MSEI 산출 결과는 <표 4>와 같이 나타났다. MSEI는 모든 지역에서 일반 반복매매지수에 비해 중첩지수가 더 작게 나타나, 중첩지수의 통계적 신뢰도가 더 높은 것으로 확인되었다. 특히 구별로 비교하면 지수산정에 이용 중인 자료수가 많은 순서대로 통계적 신뢰도가 높았으며, 일반 반복매매지수와 중첩지수의 통계적 신뢰도 간 차이는 이용 자료 수가 적은 종로구, 중구에서 더 크게 나타났다.
| 구분 | 일반 반복 매매지수 | 2개월 이동 평균지수 | 중첩 지수 | MIT/CRE 지수 |
|---|---|---|---|---|
| 강남구 | 1.120 | - | 0.859 | - |
| 종로구 | 4.172 | 2.988 | ||
| 중구 | 3.179 | 2.376 |
하지만 앞서 언급한 것과 같이 2개월 이동평균지수와 MIT/CRE 지수는 직접적으로 표준오차 산출되지 않기 때문에 통계적 신뢰도만으로는 어떤 지수산정 모형이 더 우수한 성능을 가진다고 판단을 내리는데 한계가 있다.
모형별로 SI 산출 결과는 <표 5>와 같이 나타났다. 모든 지수산정 모형에서 일반 반복매매지수가 가장 불안정한 것으로 나타났고, 중첩지수가 가장 안정적으로 산정된 것을 확인할 수 있다. 3개월 이동평균 지수의 경우, 강남구를 제외하고는 중첩지수와 비슷한 수준의 안정성을 보였고, MIT/CRE 지수는 일반 반복매매지수보다는 안정적이지만, 중첩지수나 3개월 이동평균지수에 비해서는 여전히 불안정한 지표를 보여주고 있다.
| 구분 | 일반 반복 매매지수 | 3개월 이동 평균지수 | 중첩 지수 | MIT/CRE 지수 |
|---|---|---|---|---|
| 강남구 | 0.469 | 0.578 | 0.640 | 0.555 |
| 종로구 | 0.381 | 0.683 | 0.704 | 0.595 |
| 중구 | 0.449 | 0.668 | 0.684 | 0.603 |
Revision에 관해서는 지수 값의 변화가 아닌 월 변동률의 변화를 통해 비교하였다. 지수 작성 시점이 2019년 8월인 지수부터 2018년 12월인 지수까지, 즉 2019년 8월부터 최근 월의 자료부터 하나씩 제거해 나가면서 지수산정 모형별로 총 9개의 연속된 시점에 산정된 지수를 산출하였고, 각 지수에서 가장 최근 시점의 월 변동률부터 16기간 이전 시점의 월 변동률까지 Revision을 측정하였다. Revision 지표 측정 결과는 다음의 <표 6~8>과 같이 나타났으며 s는 지수 작성 시점을 8기간 이전까지 측정하였기 때문에 8로 고정하고, n은 5가지 경우로 1부터 n기간 이전 시점까지의 Revision 전체 평균으로 RI 값을 산출하였다.
| s × n | 일반 반복 매매지수 | 3개월 이동 평균지수 | 중첩 지수 | MIT/CRE 지수 |
|---|---|---|---|---|
| 8 X 16 | 0.102 | 0.044 | 0.096 | 0.148 |
| 8 X 12 | 0.128 | 0.054 | 0.112 | 0.161 |
| 8 X 8 | 0.175 | 0.071 | 0.136 | 0.156 |
| 8 X 4 | 0.243 | 0.096 | 0.182 | 0.140 |
| 8 X 1 | 0.438 | 0.189 | 0.390 | 0.011 |
| s × n | 일반 반복 매매지수 | 3개월 이동 평균지수 | 중첩 지수 | MIT/CRE 지수 |
|---|---|---|---|---|
| 8 X 16 | 0.229 | 0.072 | 0.083 | 0.093 |
| 8 X 12 | 0.294 | 0.090 | 0.098 | 0.115 |
| 8 X 8 | 0.414 | 0.122 | 0.118 | 0.149 |
| 8 X 4 | 0.637 | 0.177 | 0.160 | 0.213 |
| 8 X 1 | 1.158 | 0.352 | 0.295 | 0.373 |
| s × n | 일반 반복 매매지수 | 3개월 이동 평균지수 | 중첩 지수 | MIT/CRE 지수 |
|---|---|---|---|---|
| 8 X 16 | 0.170 | 0.079 | 0.118 | 0.585 |
| 8 X 12 | 0.216 | 0.098 | 0.139 | 0.680 |
| 8 X 8 | 0.298 | 0.128 | 0.163 | 0.664 |
| 8 X 4 | 0.384 | 0.162 | 0.235 | 0.561 |
| 8 X 1 | 0.575 | 0.227 | 0.328 | 0.007 |
기본적으로 일반 반복매매지수는 모든 자치구에서 평균 적인 지수변화 정도가 가장 큰 것으로 나타났다. 모형별로 비교하면, MIT/CRE 지수의 경우 가장 최근 시점의 지수변화 정도가 상당히 작게 나타나고, 그 이후로는 일정 수준을 유지하는 양상을 보이고 있다. 여기에서 평균값이 아닌 최근 시점으로부터 1개 기간씩 따로 산출해 보면 MIT /CRE 2단계 추정법의 모형 특성으로 인해 3기간 당 한 번씩 지수변화가 상당히 작게 나타나는 것을 확인할 수 있다. 3개월 이동평균지수와 중첩지수는 최근 시점의 지수변화는 크게 나타나지만, 장기적으로는 점차 지수 변화 정도가 작아지는 방향으로 수렴하는 형태를 보여주고 있으며, 그 변화 정도 또한 강남구를 제외하면 크게 차이나지 않는 수준으로 나타났다. 그러나 종로구를 제외하면 대체로 3개월 이동평균 지수의 지수변화가 더 적게 나타나는 것을 확인할 수 있다.
결과적으로 최근 시점의 RI 값만을 비교하면 MIT/CRE 지수가 가장 지수변화 정도가 가장 적지만, 장기적으로 봤을 때는 3개월 이동평균 지수가 가장 지수변화 정도가 작게 나타났고, 중첩 지수도 그와 비슷한 수준으로 작은 RI 값을 나타내고 있다고 볼 수 있다.
세 가지 지표를 통해 지수의 산정 모형별로 추정 성능을 비교한 결과, 일반 반복매매지수보다는 세 가지 지수 모두 우수한 성능을 나타내었다. 그러나 MIT/CRE 지수의 경우, 3개월 이동평균 지수, 중첩지수에 비해 불안정한 결과를 만들어냈고, Revision의 측면에서도 특정 기간에서만 지수변화가 적게 나타나고, 그 외에 장기적으로는 상대적으로 큰 변화를 만들어내는 것을 확인할 수 있었다. 3개월 이동평균 지수의 경우에는 Revision의 측면에서는 가장 우수한 성능을 나타내고 있으나, 중첩지수에 비해 안정성이 떨어지고, 기본적으로 일반 반복매매지수를 이용하여 단순 평균 계산을 통해 산정된다는 점에서 중첩지수에 비해 통계적 신뢰도 또한 높다고 할 수 없다.
결과적으로 본 연구에서 제안한 중첩지수가 기존의 지수 산정 방법론에 비해 모든 측면을 고려하였을 때 보다 나은 추정 성능을 지니고 있는 것으로 판단된다. 그러나 실무에서의 적용을 위해서는 중첩 방식에 대한 추가적인 검토가 필요하다. <그림 7>은 2개월의 자료를 중첩한 경우와 3개월의 자료를 중첩한 경우에 산정되는 지수를 비교한 것이다.
강남구, 종로구, 중구의 3개 자치구에 대하여 2개월의 자료를 중첩하여 산정한 지수는 실선으로, 3개월의 자료를 중첩하여 산정한 지수는 점선으로 표현하였고, 보다 정확한 비교를 위해 가격이 안정되는 2013년 6월을 기준시점으로 하였다.
강남구 지수의 2018년 12월부터 약 4개월 정도 기간 동안 3개월 중첩 지수가 조금 더 높은 수준으로 차이가 벌어지는 부분을 제외하면 거의 모든 시점에서 지수 추이는 유사하게 나타났다. 앞서 지수산정 모형 간 비교를 위해 도입하였던 통계적 신뢰도, 지수 안정성, 지수변화의 지표의 경우에는 3개월 중첩지수가 한 시점의 지수 산정을 위해 보다 많은 자료를 이용함으로써 더 우수한 지표 값을 나타내었다. 그러나 <그림 8~10>에서 보여주는 월 변동률 양상의 차이는 또 다른 결과를 보여주고 있다.
세 개의 자치구 모두 대부분의 기간 동안 월 변동률의 폭이 2개월 중첩지수에 비해 3개월 중첩지수가 더 작게 나타났다. 지수의 추이가 유사함에도 불구하고, 월별 가격 변동 폭이 작게 나타나는 것은 그만큼 지수가 평활화 되었다는 것을 의미하기도 한다. 지수 안정성 지표가 클수록 더욱 안정적인 지수이기도 하지만, 일정 수준의 안정성 이상에서는 이러한 현상이 오히려 문제가 될 수도 있다. 지수가 지나치게 평활화 될 경우, 시장 가격의 변동을 적시에 제대로 담아내지 못하게 되며, 지속적으로 누적되면서 장기적인 추세가 실제 가격 변동의 추세를 벗어나는 문제가 발생할 수 있다. 이러한 이유로 실무적으로 중첩 지수를 적용하고자 할 때 2개월의 자료를 중첩하는 방식이 적절한 것으로 판단된다.
Ⅴ. 결론
본 연구는 2006년 1월부터 2019년 8월까지 신고된 서울시 아파트 실거래가 자료를 이용하여 강남구, 종로구, 중구와 같이 상대적으로 이용 가능한 자료 수가 부족한 하위시장의 실거래가 지수를 산정하였으며, 이를 위해 여러 개월의 자료를 중첩하여 실질적으로 지수 산정에 이용하는 자료 수를 증가시킴으로써 안정적인 지수 산정을 가능하도록 하는 자료처리방식을 제안하였다. 또한 중첩지수의 성능을 평가하기 위해 가장 기본적인 반복매매모형과 더불어 이동평균 지수, MIT/CRE 지수와 같이 보다 안정적인 지수 산정이 가능한 기존의 모형들과 비교 분석하였다.
지수의 추정성능을 평가하는데 중요한 요소로 판단되는 통계적 신뢰도, 지수 안정성, 지수변화(Revision)의 세 가지 지표에 대하여 비교한 결과, 일반 반복매매지수에 비해 다른 세 가지 모형 모두 우수한 추정 성능을 나타내었다. 해당 세 가지 모형 간에 비교하였을 때는 비교 지표별로 조금씩 다른 양상을 보였는데, 통계적 신뢰도에 있어서는 이동평균지수, MIT/CRE 지수의 경우 직접적인 표준오차 산출에 어려움이 있으나 중첩지수의 통계적 신뢰도가 가장 우수한 것으로 판단된다. 지수 안정성의 측면에서는 중첩지수, 이동평균 지수, MIT/CRE 지수의 순으로 안정적인 지수가 산정되었으며 이는 지수 그래프를 통해서도 확인할 수 있었다. 지수변화의 경우에는 MIT/CRE 지수의 최근시점 지수변화가 상당히 적게 나타나는 특징이 있었고, 종로구를 제외하면 대체로 이동평균 지수의 지수변화 정도가 가장 적게 나타나는 것을 확인할 수 있었다. 결과적으로 MIT/CRE 지수는 모형 특성상 초기 3개 시점의 지수 산출에 한계가 있고 1분기 정도의 시차가 발생한다는 점, 지수변화의 정도는 이동평균 지수가 가장 적게 나타나지만 중첩지수의 지수변화 지표가 수용 가능한 수준에서 크지 않은 차이를 보이는 점, 그리고 통계적 신뢰도와 지수 안정성 측면에서 가장 우수한 추정성능을 보여준다는 점에서 중첩지수의 실제 활용 가능성을 확인할 수 있었다. 다만, 3개월 이상 자료 중첩을 할 경우 지나치게 지수가 평활화 될 수 있는 문제가 있어 2개월의 자료를 중첩하는 방식을 실무적으로 적용하는 것도 지수의 안정성이 보장되는 하부시장 구분의 경우 현실적인 대안으로 판단된다.
이러한 분석 결과는 본 연구에서 제안한 자료 중첩 방식의 다양한 활용 가능성을 보였다는 점에서 의의가 있다. 분석과정에서 시도하였던 것과 같이 세분화 된 지역적 하위 시장뿐 아니라, 기본적으로 아파트만큼 거래가 충분히 관측되지 않는 단독·다가구 및 연립·다세대 주택, 혹은 주 단위 등 thin market 혹은 granular market이라고 일컬어지는 대상에 대한 지수 산정을 가능하게 함으로써 시장에 보다 정확하고 다양한 정보를 제공할 수 있다. 또한 특정 모형을 적용하는 것이 아닌 자료처리 방식을 달리하는 것으로 분석에 이용하였던 동일가중-기하평균 반복매매모형 이외에도 지수의 목적과 활용용도 등에 따라 다른 모형에도 폭넓게 적용할 수 있다는 장점이 있다.
그러나 분석을 수행함에 있어 지수의 추정성능을 비교하는데 이용한 지표 중 이동평균 지수와 MIT/CRE 지수에 대하여는 직접적인 표준오차 산출에 한계가 있어 직접적으로 통계적 신뢰도의 비교가 어려웠고, 지수변화는 모형별로 각기 다르게 나타나는 특성에 대한 명확한 설명을 담아내지 못했다는 점에서 한계점이 있다. 반복매매모형의 특성상 구조적으로 불가피하게 나타날 수밖에 없는 지수변화의 경우 특정 기간의 지수변화는 자료의 해당시점 특성에서부터 나타날 수 있으나, 장기적인 지수변화 추세는 모형의 특성에서 기인한 것으로 생각되는데 이에 대한 추가적인 연구가 필요하다.